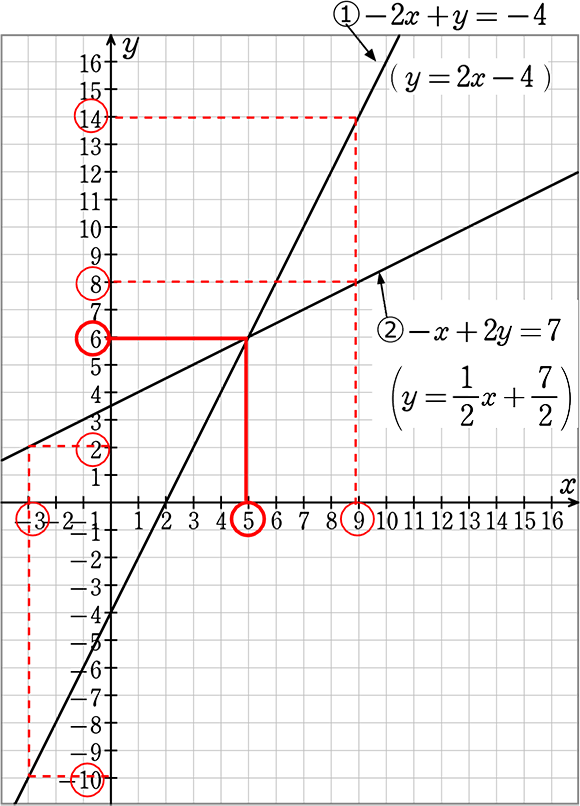
連立方程式1 D SML01 次の各問いに答えなさい。ただし,解答用紙には答えだけでなく,解き方も示すこと。(配点 50) x次の①~③の連立方程式のうち,解が =-2,y=-3 であるものはどれですか。 番号で答えなさい。連立方程式の解はこの 2 つの式を同時にみたす点の集合であるらか, 2 つの直線の交点が連立方程式の解となる. 交点をもつ条件は次の 3 つに分けられる.連立方程式とは 連立方程式を簡単に説明すると 「複数の解を求めるための、複数の方程式を組み合わせた式」 です。 たとえば 「A君はB君の2倍の年齢である」 これをA君がx歳、B君がy歳として方程式を立てると、 \(x=2y\) となります。しかし未知の文字が2つあるのでこれだけでは解の候補が
Q Tbn And9gcrxeqtkfzspr84pbplx9xl09lwn 7v64y00sc7qxffojd2h H0u Usqp Cau
連立方程式 3つ
連立方程式 3つ-2元1次方程式や連立方程式の意味を理解し、代入法や加減法で、連立方程式を解く練習をする問題プリントです。 連立方程式の解き方 練習問題 (1) 答え 連立方程式の解き方 練習問題 (2) 答え 連立方程式の解き方 練習問題 (3) 答え 連立方程式の測定された2波長赤外線カメラ3の出力値をこの関係式に代入し、2元非線形 連立方程式 を解くことにより、目標の温度及び距離を求める。 例文帳に追加 A measured output value from the twowavelength infrared camera 3 is substituted for the relational



5 1 連立方程式 基本 勉強できようサイト
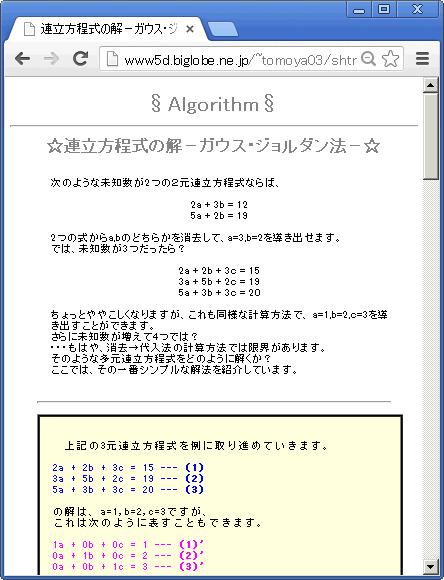
この記事では特殊な形の 連立方程式 の 解き方 について解説します。 高校数学では特殊な連立方程式がいくつか存在します。 これらは解き方にも特徴があり、一度経験しておくのが理想的です。 特殊な連立方程式は、様々な問題を解く過程で出てきますこの例題の,(35)式の形に至るまで(すなわち,解がそれぞれ求まるまで)3つの演算を行う 解法を GaussJordan の消去法という.消去法は,変数の数が増えても有効な解法である. ところで,連立1次方程式(31)を行列の式で表すと本日のお題 連立線形微分方程式 \(\left\{\begin{array}{l} x' = ax by \\ y' = cx dy \end{array}\right\) について いずれか一方の関数の線形2階斉次微分方程式に帰着させて解くことができるようになりま
連立方程式 2つ以上の方程式を組み合わせたものを,連立方程式という。 中学2 年で学習するのは,次のような,2 つの2 元1 次方程 式を組み合わせたものである。 (x − 4y = 8 3x 2y = −4 2 つの方程式を同時に成り立たせるx とy の値の組を,連立試験問題連立方程式1 試験問題連立方程式2 試験問題A=B=C型 試験問題まとめ → 携帯版は別頁 連立方程式(高校入試問題) 15年~17年の公立高等学校入試問題で,連立方程式の計算問題として出題されたものを以下のA~Gの型に分類すると,右のグラフのような割合になります. すなわち,Bの型の問題が最も多く出題されており,受験勉強の時間が足りなけれ 連立方程式の解とは、二つの方程式を同時に満たす解です。 ①②の連立方程式の解は①②の共通の解になっています。 ①②の共通の解は③④でも共通の解になっています。 ⑫②の連立方程式の解は、③④の連立方程式の解になります。
正直、連立方程式の文章題なんてクソクラエと思ってたよ笑 今日は、そんな中学生のために、 連立方程式の文章題の解き方 をわかりやすく解説してみたよ。 よかったら参考にしてみてね^^ 連立方程式の文章題の解き方がわかる3ステップ このように3つ文字を含むような連立方程式のことを、連立3元1次方程式といいます。 この場合には、 文字を1つずつ消去して解いていきましょう。 まずは、最初に消去する文字を決めます。 係数が揃ってる、揃えやすそうな文字から消去していきましょう。 3列目、4列目はこれ以上掃き出せない。 対応する方程式は、 \left\ { \begin {array} {l}x\phantom {y}3z\phantom {2}w=\phantom {}5\\\phantom {x}y2z2w=4\end {array}\right \left\ { \begin {array} {l}x=3ab5\\y=2a2b4\\z=a\\w=b\end {array} \right が一般解となる。



ちょっと複雑な連立方程式を練習しよう インターネット家庭教師のアスミラ



U9j580gf8iba369ji2w Xyz P 703
連立方程式とパラメータ 前回習った方法(基本変形) を次の方程式に適用すると, 係数行列を単位行列まで 変形できない 例31 連立方程式 (x2y = 2···⃝1 2x4y = 4···⃝2 ···(♡) の拡大係数行列A˜ に対し, A˜ = 1 2 2 2 4 4 ⃝2 −2×⃝1 −−−−−−→ 1 2 2 0 0 063 プログラム・コーディング この操作をプログラムとして実現するには、どうすれば良いだろうか? また、一般にn元の連立方程式を解く場合には、どのようなプログラムを記述すれば良いだろうか?解説 3 (2xy)=3x7y23 分配法則でカッコを開くと 6x3y=3x7y23 6x3y=3x7y23を 整理して3x10y=23 2 (3x7y)7x=27 分配法則でカッコを開くと 6x14y7x=27 6x14y7x=27を 整理してx14y=27 x14y=27の両辺に3をかけ、辺々たすと 3x10y = 23 ) 3x42y = 81 52y = 104




Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




連立方程式で3つの式のある3元1次方程式とは 3元連立方程式の解き方をわかりやすく解説 Himokuri
連立方程式の問題を3問解説します。 目次 簡単な問題 例題1 代入法による答え 加減法による答え 普通の問題 例題2 加減法による解答連立方程式(代入法) 連立方程式(加減法1) 連立方程式(加減法2) 連立方程式(かっこのある式) 連立方程式(a=b=c) 連立方程式 解と係数 連立方程式 解と係数2 文章題 代金と個数 文章題 代金と個数2 文章題 速さ1 文章題 速さ2 文章題 速さ3 文章題速さ 往復 文章題速さ 出会う追いつく 文章題速さ 長さのあるもの 文章題 2けたの自然数 文章題 商と余り 文章題 濃度の問題 文章** a=b=c 型の連立方程式(入試問題) ** 〇このページで扱う方程式は「芋づるのように」「イコールが連なっている」のが特徴です.




Math 超簡単 連立方程式の利用 働きアリ




3つの連立方程式の問題 解き方はこのようにすればバッチリだ 中学や高校の数学の計算問題
問題8で行った変形は次の3つである。これらは連立1次方程式の基本変形と呼ばれる。 (1) 1つの式を何倍か(6= 0 倍)する。 (2) 2つの式を入れ替える。 (3) 1の式に他の式の何倍かを加える。 3 基礎知識とポイント 今まで解いてきた連立方程式は「x」と「y」の2つの文字だったよね? でも今回は「x」と「y」と 「z」 の3つの文字がある! これだと、普通に解けないよね? そういう時は、 文字を1つ消す んだ! ! 手順は、 消しやすい文字を見つける 「消しやすい文字を消した式」を2つ作る 2 連立方程式の解き方のすべての基本! 「代入法」と「加減法」 21 連立方程式の解き方基本:加減法 22 連立方程式の解き方基本:代入法 23 連立方程式「x2y = 2xy9 = 11」の解き方 24 文字が3つ出てくる連立方程式の解き方 3 文字同士のかけ算が入る



連立方程式の未知数が4つでも 係数を見比べることで 解く前に解き方を決める子に育てることが可能です 計算が得意な子に育てる効果的な教え方




1 と 3 の解き方と答えがわかりません 教えてほしいです Clear
するとこの連立方程式は、 \begin {eqnarray}\left\ {\begin {array} {l}4a2b=2\\4b2a=8\end {array}\right\end {eqnarray} となります。 これは連立方程式と変わりませんから、同じように解いていきます。 a と b の位置を入れ替えると、 \begin {eqnarray}\left\ {\begin {array} {l}4a2b=2\\2a4b=8\end {array}\right\end {eqnarray} となります。連立方程式に対する以下の変形を基本変形という。 1 1次方程式を何倍かする。(0倍はのぞく。) 2 2つの方程式を交換する。 3 ある方程式に別の方程式を何倍かして加える。 これを行列の変形の言葉に変えると以下のようになります。連立方程式(加減法3) 連立方程式を解け 3x4y=6 4x3y=17 5x8y=23 8x3y=27 2x7y=6 5x6y=8 8x3y=15 9x7y=48 11x3y=37 6x5y=60 9x7y=29 7x3y=31 4x5y=18 6x7y=26 5x6y=72 7x8y=98 12x13y=17 16x15y=11 9x14y=16 6x5y=11 8x15y= 10x21y=34 24x25y=27 16x27y=49
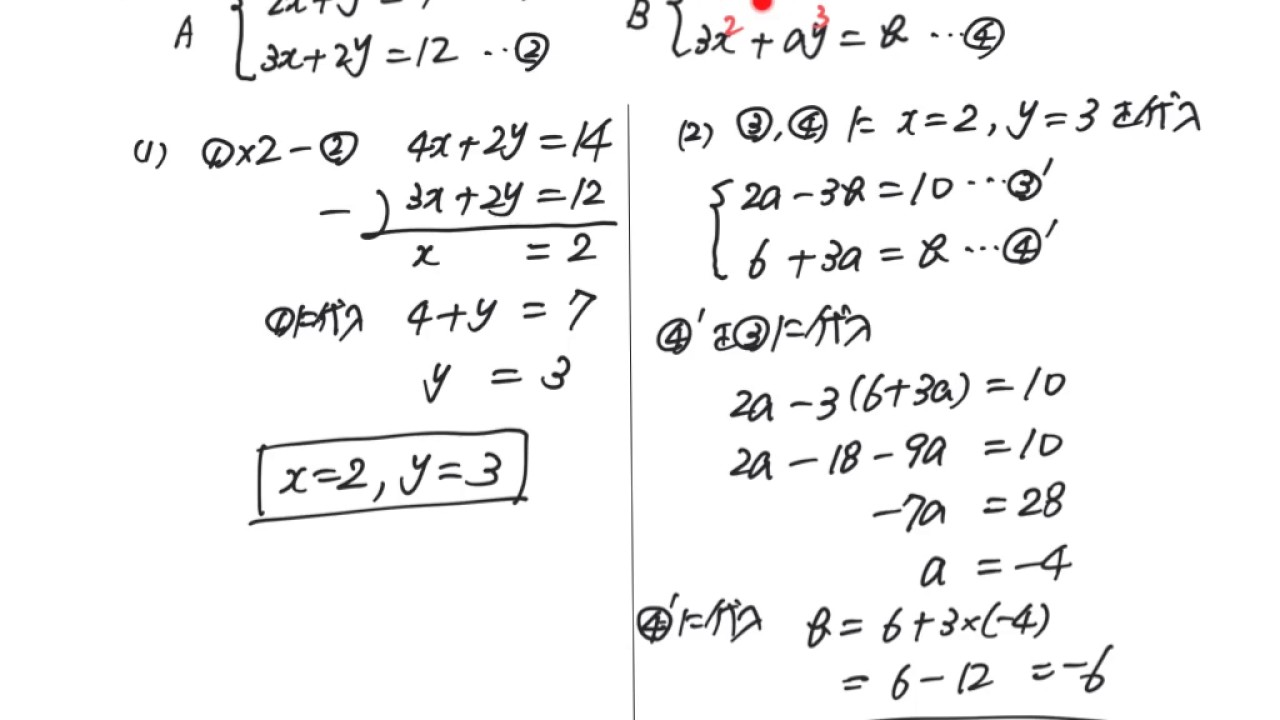



中2数学連立方程式 4つの式が同じ解を持つ Youtube
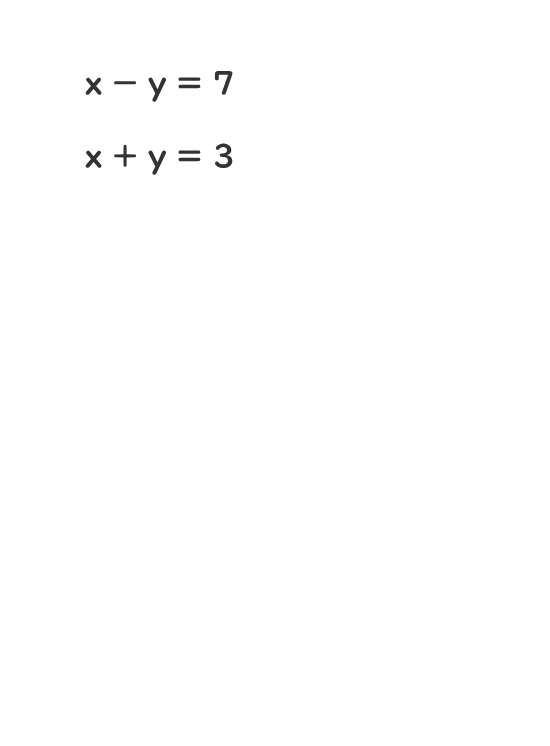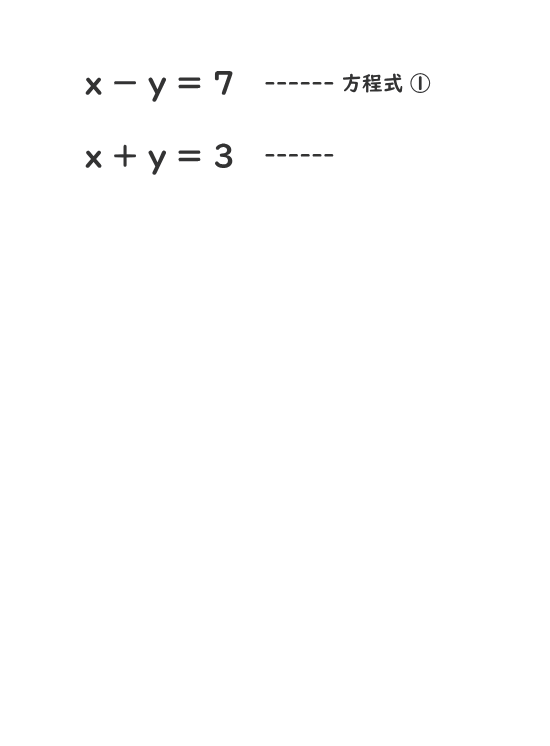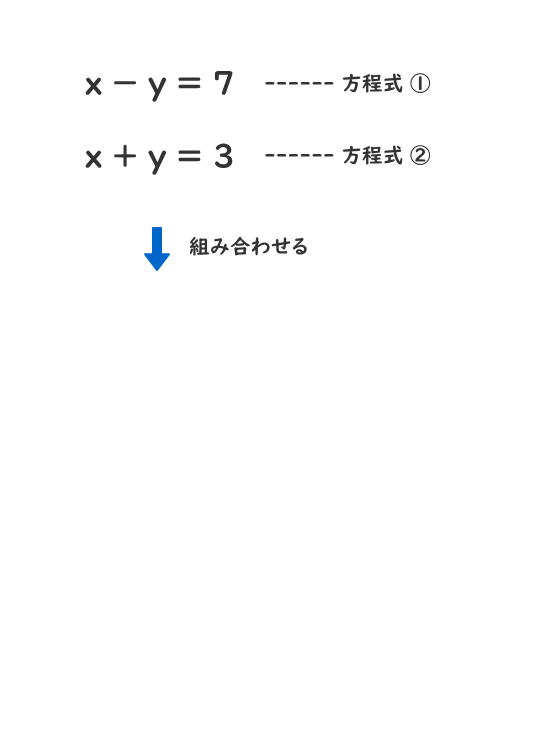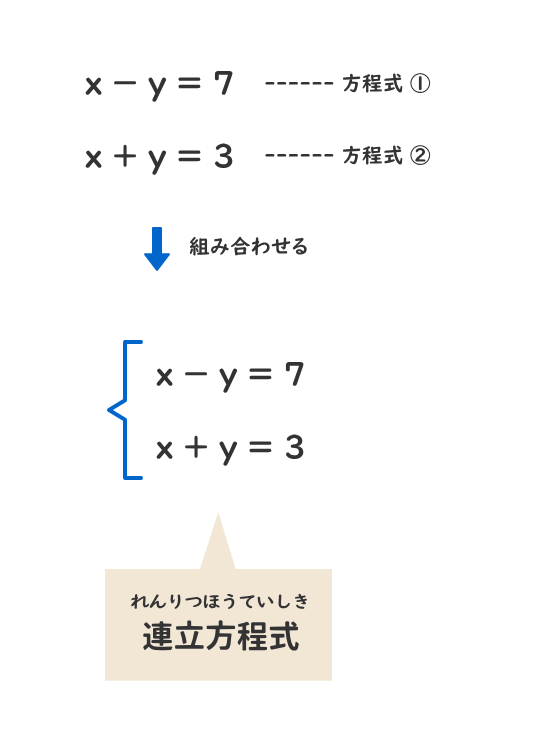



連立方程式の解き方 電験3種web
となり, 上と同様の理由で, この連立方程式は上の連立方程式と同じ解をもつ さらに, この連立方程式の2 番目 の式と3 番目の式を入れ替え, 新しい3 番目の式の両辺を5 で割ると, 8 >> >< >> > x¡3z ¡11w = 4 y z 5w = ¡2 z 5w = ¡3 となる① ×3-②9x−3y=15 − ) 2x−3y=−6 7x=21 x=3 x=3を①に代入して9−y=5 y=4 (1) ( ,y)=(−1,4) (2) ( ,y)=(3,4) 4 次の連立方程式を解きなさい。 ({2(3 −2 )− =0 ① 4( +2)−3( −2)=16 ② かっこをはずすと {6 −4 − =0 4 +8−3 +6=16定義 3 8 (連立 1 次方程式の基本変形) 連立 1 次方程式に対する次のの操作を 連立 1 次方程式の基本変形と呼ぶ. (1) 一つの式を 倍する. (2) 二つの式を入れ替える. (3) 一つの式を 倍して別の行に加え
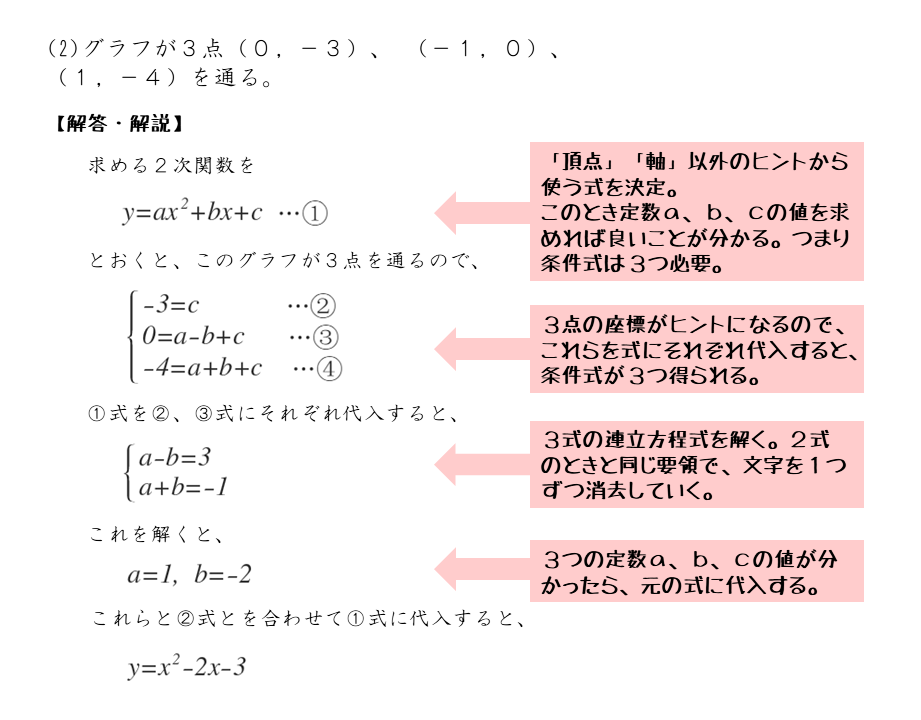



2次関数 2次関数の決定について 日々是鍛錬 ひびこれたんれん




中2 数学 連立方程式の解き方二通りを解説 授業動画あり アオイのホームルーム
下記の3元連立1次方程式を考えよう。 (変数は x 1, x 2, x 3) 5x 1 3x 2 x 3 = 3 4x 1 5x 2 2x 3 = 4 x 1 3x 2 6x 3 = 6 とおき、マトリックスで表記すると、極めて簡単に連立方程式(代入法) 連立方程式(加減法1) 連立方程式(加減法2) 連立方程式(かっこのある式) 連立方程式(a=b=c) 連立方程式 解と係数 連立方程式 解と係数2 文章題 代金と個数 文章題 代金と個数2 文章題 速さ1 文章題 速さ2 文章題 速さ3 文章題速さ 往復 文章題速さ 出会う追いつく 文章題速さ 長さのあるもの 文章題 2けたの自然数 文章題 商と余り 文章題 濃度の問題 文章 3元連立1次方程式(一般型と循環型) 次の連立方程式を解け xy=12 & yz=13 & zx=15 {3元1次連立方程式} {加減法}で求めるのが普通である\ まずはとから消去しやすいzを消去する この後,\ とから消去しやすいyを消去する人が多いが,\ 最悪中の最悪である {連立方程式の大原則は1文字消去である\ 1文字を徹底的に消去するのである y消去の誘惑に駆られてはならない




中2数学 a b cの連立方程式 練習編 映像授業のtry It トライイット




中学数学 連立方程式 の効果的な教え方 導入と指導上の注意点
線形代数1・第6 回(21 年5 月18 日) 授業用アブストラクト 0 @ a1 b1 c1 0 a2 b2 c2 0 a3 b3 c3 1 1 A ⃝2 1⃝ (a2 a1 ⃝3 1⃝ (a3 a1 0 @ a1 b1 c1 0 0 a1b2 a2b1 a 1 a1c2 a2c1 a 0 0 a 1b 3 a b a1 a c a c a1 1 1 A となるから、AX = の第2 列と第3 列を取り出して作られる連立一次方程式から、 a1b2 a2b1 a1 a1c2 a2c1 a1 a1b3 a3b1 a1 a1c3 a3c1 a1三元連立方程式 自分の計算が不安で利用させていただきました。 思っていたより間違ってたので使ってよかったです。 4元にも対応してくれたら大変有難いです。 世界の経緯度観測所のデータ(3か所)から、形状軸からの極 (瞬間自転軸)のズレの計算に三元連立方程式 自分の計算が不安で利用させていただきました。 思っていたより間違ってたので使ってよかったです。 4元にも対応してくれたら大変有難いです。 世界の経緯度観測所のデータ(3か所)から、形状軸からの極 (瞬間自転軸)のズレの計算に




三元連立方程式 1 中2数学 Youtube
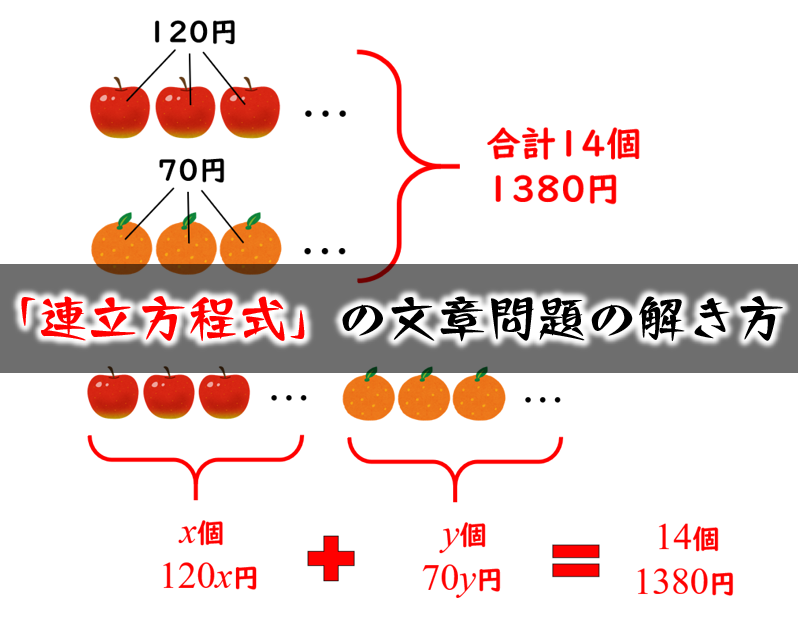



連立方程式の文章問題の解き方 数学fun




連立方程式 A B Cの3つ式があるときの解き方を解説 中学数学 理科の学習まとめサイト




Line Blog 芸能人 有名人ブログ



連立方程式の代入法 大人の学び直し算数 計算のやり方解説 無料




連立方程式を解く時の流れを行列に当てはめてみよう 線形代数を宇宙一わかりやすく解説してみるサイト



連立一次方程式 を高速に効率よく解くために 計算基礎科学連携拠点



連立方程式の加減法 大人の学び直し算数 計算のやり方解説 無料




連立方程式編 解の条件 大学1年生もバッチリ分かる線形代数入門



掃き出し法で連立方程式を解く手順とコツを解説




4元連立方程式を解く際に気をつけるべきポイントは何でしょうか Clear




問題3 連立方程式を解くプログラムを作れますか Pythonで学び直す高校数学 エンジニアtype 転職type




3分で分かる 式が3つの連立方程式の解き方をわかりやすく解説 合格サプリ




連立方程式 X Y 3 Xy 2の和と積の方程式の解き方は 数スタ




連立方程式で式が三つあるものはどう解けばいいのですか Clear




高校数学 3元連立1次方程式 一般型と循環型 受験の月



連立方程式の解き方を徹底解説 中学数学からセンター試験まで Studyplus スタディプラス




クラメルで連立方程式 その2 大学の数学 超入門シリーズ Youtube




コミック 数学サバイブ物語 連立方程式 二つの式がある理由 端野 洋子 ブルーバックス 講談社 6 6



連立方程式の文章題 代金 チーム エン



1



中3 二次方程式の基本解説 中学数学の方程式 中間 期末テスト 高校入試対策



連立方程式の解き方を徹底解説 中学数学からセンター試験まで Studyplus スタディプラス



連立方程式とは 代入法と加減法 計算問題や文章題の解き方 受験辞典




連立方程式の2つの解き方 代入法 加減法 数学fun



Q Tbn And9gcrxeqtkfzspr84pbplx9xl09lwn 7v64y00sc7qxffojd2h H0u Usqp Cau




中学2年数学 連立方程式 加減法を使った連立方程式の解き方 実際に問題を解きながら解説 数学の面白いこと 役に立つことをまとめたサイト
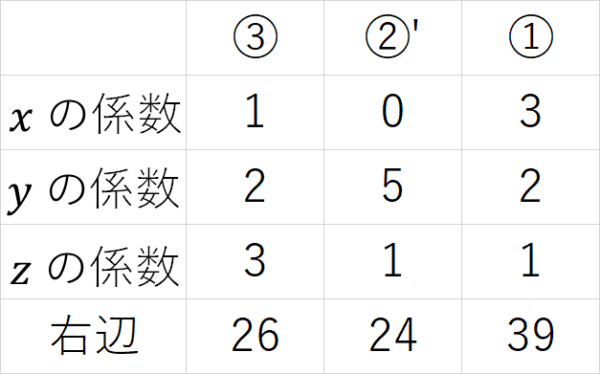



数学史5 4 紀元前の中国 連立方程式 Fukusukeの数学めも




整数解をもつ連立3元2次方程式を解こう 2017年度前期日程の一橋大学入試問題 身勝手な主張
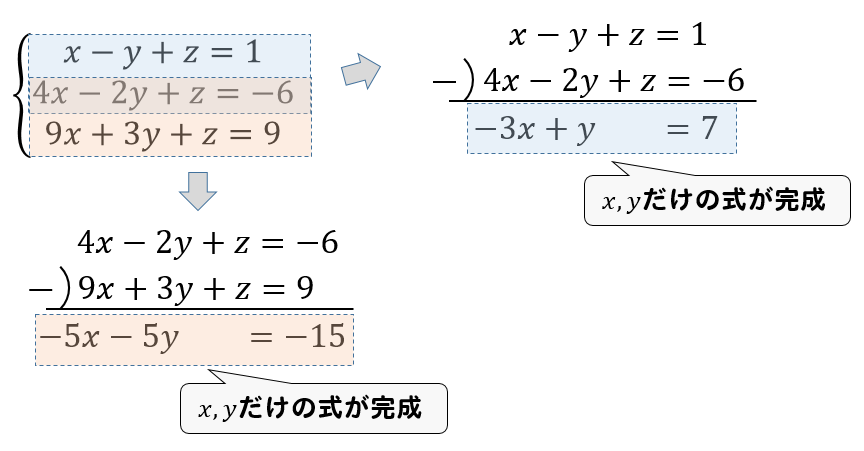



連立方程式3つあるときの計算方法は 例題を使って解き方を解説 方程式の解き方まとめサイト




連立方程式を行列で解く その仕組みをわかりやすく解説




3分で分かる 式が3つの連立方程式の解き方をわかりやすく解説 合格サプリ




徹底解説 連立方程式の解き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく



中学数学 連立方程式 二元一次



数学の連立方程式についてです 写真のように 文字2つで3つ で連な Yahoo 知恵袋



5 1 連立方程式 基本 勉強できようサイト



中2 連立方程式 二元一次連立方程式 の基本解説 中学数学の方程式 中間 期末テスト 高校入試対策




高校数学 2元2次連立方程式3パターン 受験の月




この連立方程式がどうしても解けないです Clear




連立方程式の利用 その 苦手な数学を簡単に



21 中学数学 連立方程式 計算問題 Pc Android App Download Latest



未知数が x y z の3つの連立方程式です y に付いている数 係数 だけを2倍にすると y の答えは どうなるでしょうか 計算が得意な子に育てる効果的な教え方




1 ありがとう 位置情報 連立方程式 オトナのための中学数学 天狼院書店




中2数学 a b cの連立方程式 練習編 映像授業のtry It トライイット




ちょっと複雑な連立方程式を練習しよう インターネット家庭教師のアスミラ




例題 連立3元1次方程式の解き方 Youtube




未定係数を含む3元連立方程式の解 数学解説ブログ つくば市の 数学 算数 物理に強い プロ家庭教師 長通幸大 発信




りんだろぐ Rindalog 行列で解く Systems Of Linear Equations




Begincases3x Y14x 3y7en Descubre Como Resolverlo En Qanda




連立方程式 条件を 考えて 複数の答えを 絞り出す 名寄 算数数学教室より



Studydoctor三元連立方程式 1 中2数学 Studydoctor



Pl Pgsql で多元連立方程式を解く 研究に使うポスグレ




ある連立3元3次方程式を解いてみよう 身勝手な主張




教科 オリジナル連立方程式を作ろう 答えが1つでない課題に協力して取り組む 明法中学 高等学校 明法ニュース
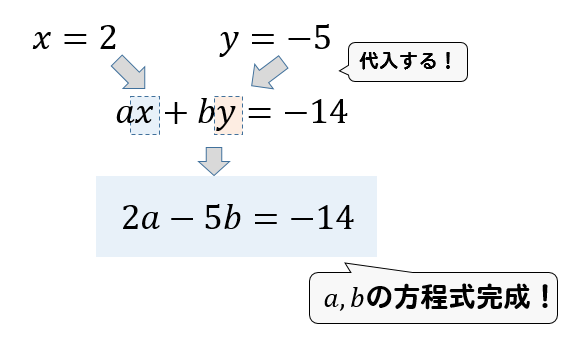



連立方程式の解が与えられている問題の解き方は 方程式の解き方まとめサイト



Q Tbn And9gcrxeqtkfzspr84pbplx9xl09lwn 7v64y00sc7qxffojd2h H0u Usqp Cau




中学2年生 数学 連立方程式の解き方 練習問題プリント 無料ダウンロード 印刷 ちびむすドリル 中学生




コンプリート 3 つの 連立 方程式 の 解き方 ニスヌーピー 壁紙
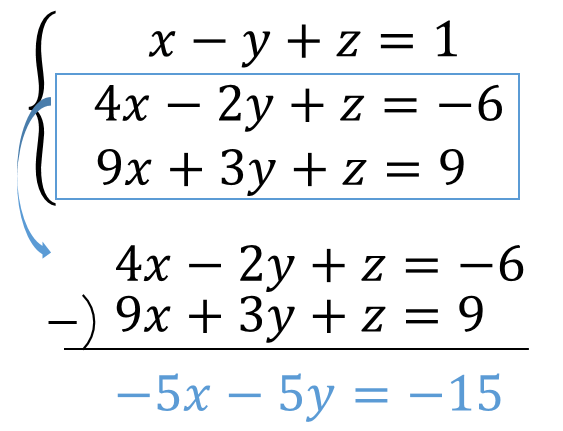



連立方程式 3つの文字 式の問題を計算する方法は 数スタ




4元連立方程式の解き方を教えてください 1 x y z W 2 2 x 数学 教えて Goo




連立方程式とは 中2数学 Enjoy Study 神松寺校 福岡市城南区神松寺の個別指導学習塾




第4回講義 基礎数学



1




有機化学の一問一答bot 構造式 反応式 アプリ 計算式をスキャンして解答や解法を調べるアプリがmicrosoftから出ていました 連立方程式の解法を 代入法 行列を使用 消去法 の3つを出してくれました 多言語対応です T Co Hmjnqanvz9




連立方程式の解き方を説明しますー代入法を使った解き方ー おかわりドリル




連立方程式の解き方 加減法 代入法と文章題の計算方法 リョースケ大学



Begincasesx2yz2x Y 2z5x Descubre Como Resolverlo En Qanda




2次関数26 連立3元1次方程式 怜悧玲瓏 高校数学を天空から俯瞰する




連立方程式で3つの式がある時の解き方が誰でも分かる 高校生向け受験応援メディア 受験のミカタ




連立方程式とその解 二元一次方程式とは何もの Qikeru 学びを楽しくわかりやすく




Line Blog 芸能人 有名人ブログ




3分で分かる 式が3つの連立方程式の解き方をわかりやすく解説 合格サプリ




連立方程式の解き方とは 代入法か加減法で計算しよう 分数の問題や文章題アリ 遊ぶ数学




お勉強 連立方程式を楽に解く 数学は楽してなんぼ そらの暇つぶしch




中学数学 連立方程式 の効果的な教え方 小数 分数問題



第1章 連立方程式
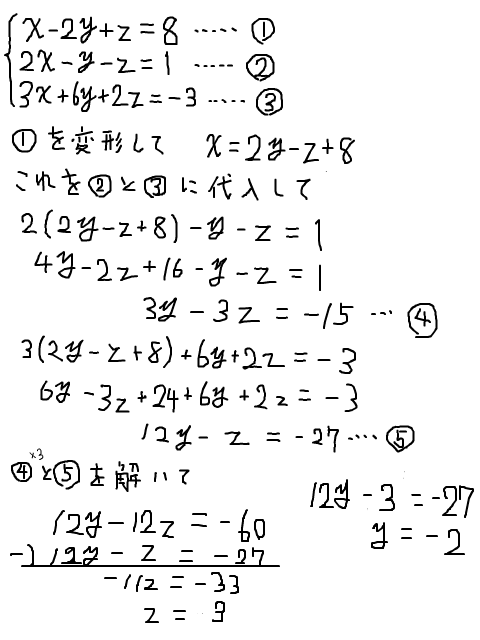



きゃおす 連立3元1次方程式 解いてみた 手書きブログ




高校数学 2式が互いに対称な連立方程式 和と差で組み直せ 受験の月




書記が数学やるだけ 44 逆行列を求める 2 余因子行列 行列のランク 連立方程式 3 クラメールの公式 鈴華書記 Note




Xyz 3つの式の連立方程式の解き方がわかる4ステップ Qikeru 学びを楽しくわかりやすく




連立方程式 1 代入法と加減法 バカでもわかる 中学数学



2 の三元一次連立方程式が 何度やっても答えが合いません 計算お願いし Yahoo 知恵袋
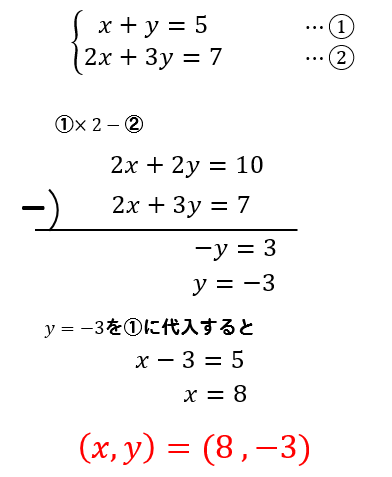



方程式練習問題 連立方程式 A B C 方程式の解き方まとめサイト




中学2年生 数学 無料問題集 連立方程式を加減法で解く おかわりドリル



連立方程式の行列解




中学数学 連立方程式 加減法 中学数学の無料オンライン学習サイトchu Su



連立方程式の行列解




かっこを含む連立方程式 解き方をイチから解説してくぞ 中学数学 理科の学習まとめサイト




連立3元一次方程式でこのように詰んでしまいます Clear



この問題は3つの式をそれぞれ60倍して連立方程式を解くでもあっていますか Yahoo 知恵袋



0 件のコメント:
コメントを投稿