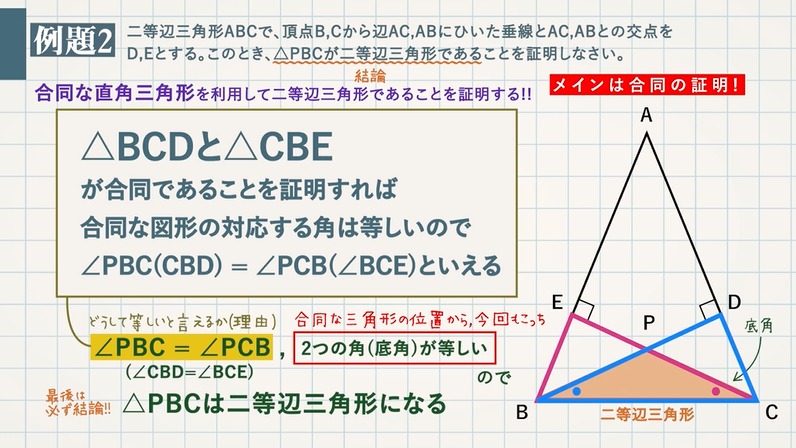
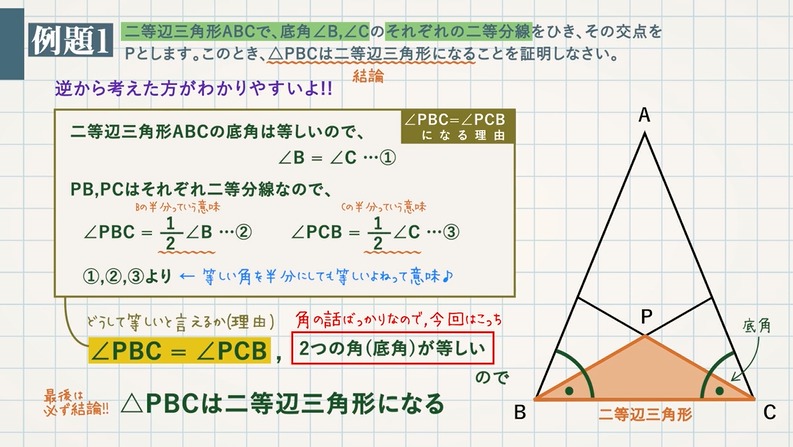
二等辺三角形であることの証明 二等辺三角形の定義性質 教遊者
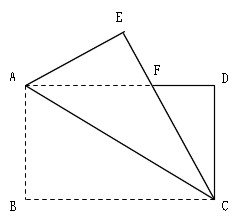
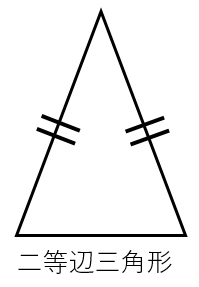
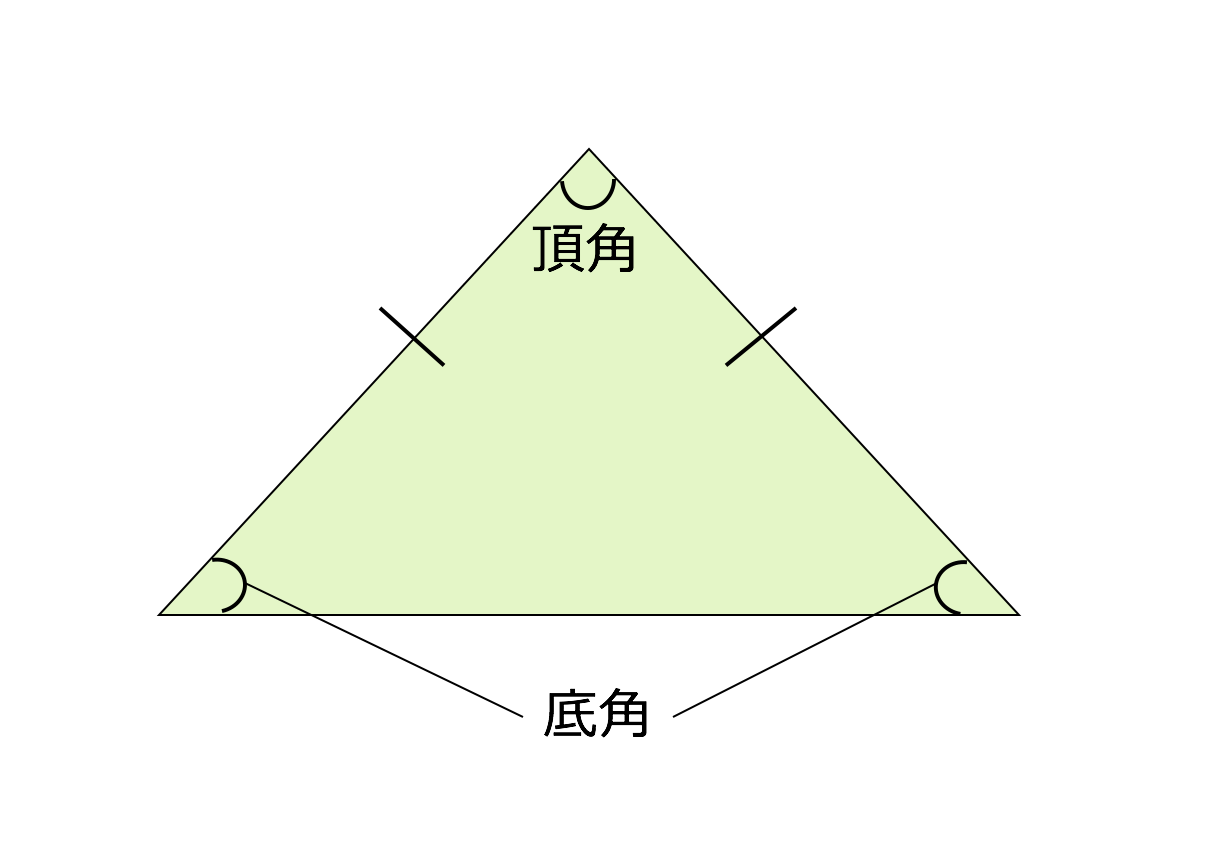
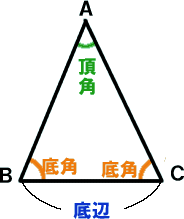
二等辺三角形の等しい \(2\) 辺の間の角を「頂角」、その他の \(2\) つの角を「底角」といいます。そして、頂角に向かい合う辺を「底辺」といいます。 二等辺三角形の定義は、その名解説 BEF B E F は見た感じ二等辺三角形ですが、どのように証明したらよいのでしょうか。 ・ 2 2 つの辺が等しい ・ 2 2 つの角が等しい のいずれかがいえればよいのです。 よって、等しい辺や角
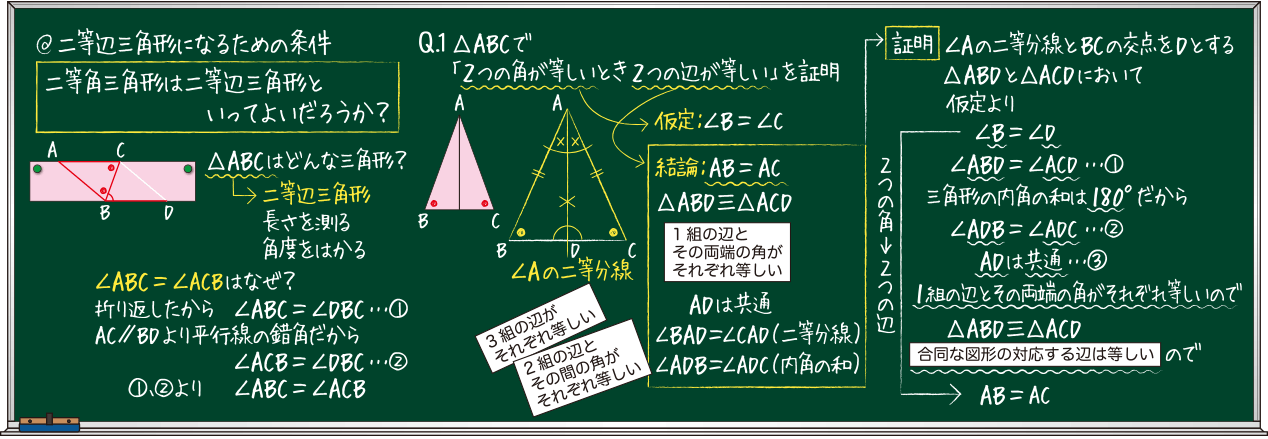
二等辺三角形になるための条件 証明
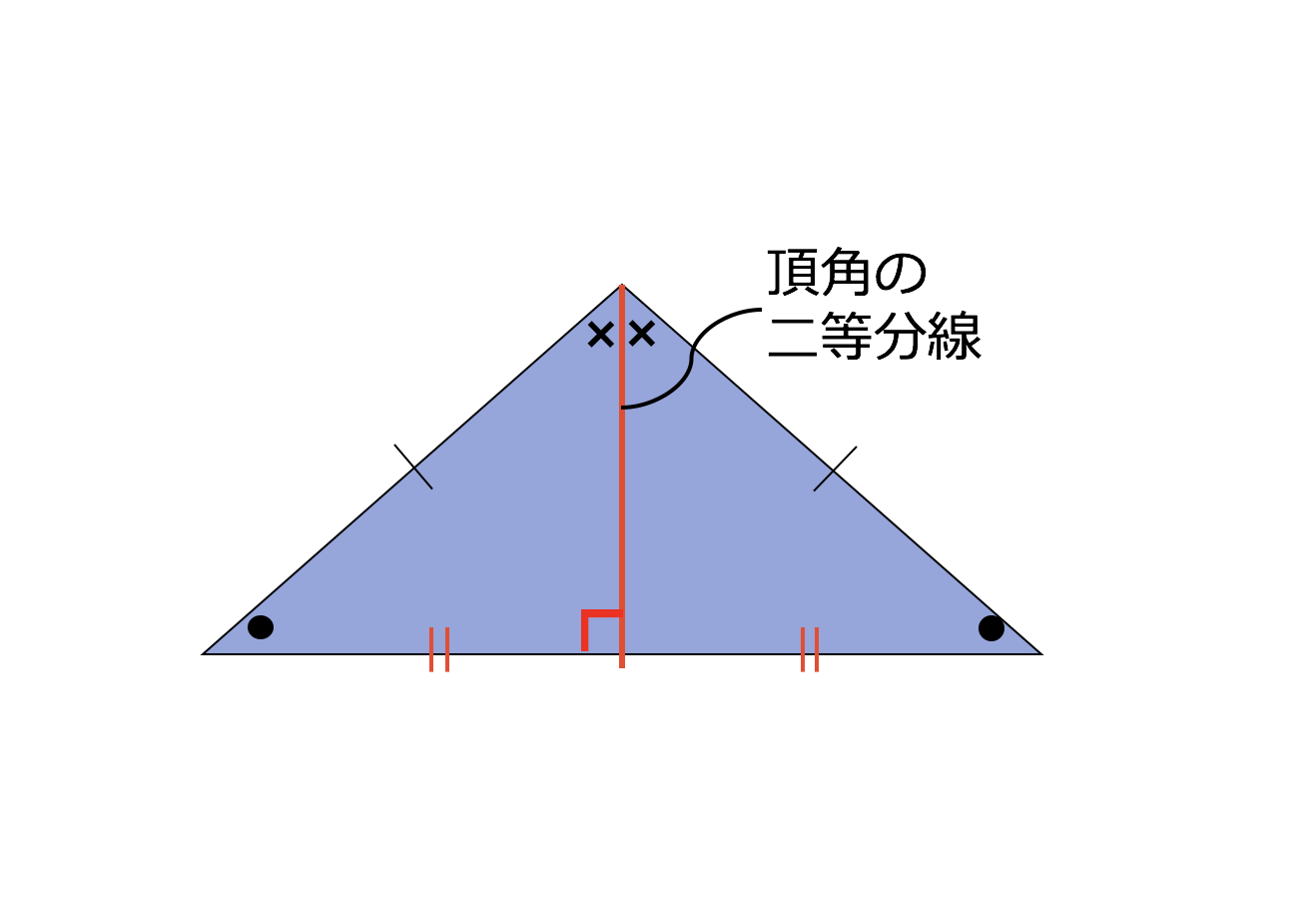
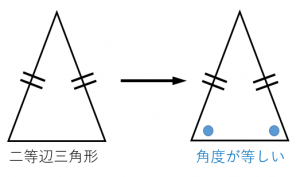
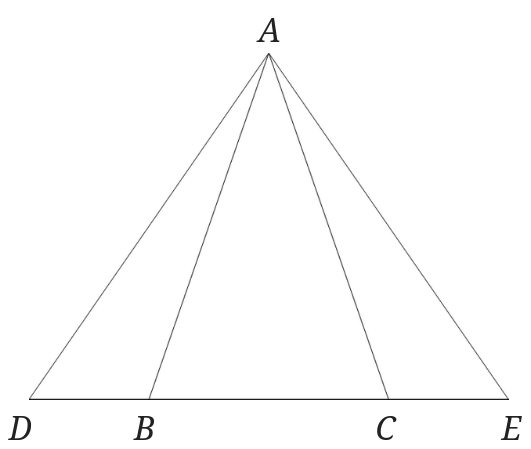
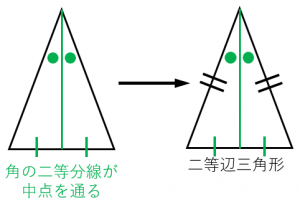
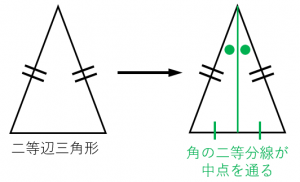
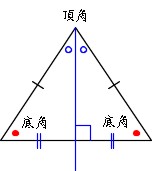
二等辺三角形になるための条件 証明-$\textcolor{blue}{2}$ :頂角の二等分線は、底辺を垂直に二等分する 二等辺三角形になるための条件 (定義と定理を使う) ・ $\textcolor{blue}{2}$ 辺が等しい ・ $\textcolor{blue}{2}$ つの角(底角)二等辺三角形になるための条件(1) 二等辺三角形になるための条件 定理 三角形の2つの角が等しければ、その三角形は等しい2つの角を底角 とする二等辺三角形である。 1 下の図のように、AB=ACの二等辺三角形ABCの辺AB,AC上にそれぞれ
3分で分かる 二等辺三角形の特徴 角度 辺など についてわかりやすく 合格サプリ
5 9 1 回答 教科書に「二等辺三角形になるための条件」として、定理「三角形の2つの角が等しければ、その三角形は、等しい2つの角を底角とする二等辺三角形であるAbout Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy & Safety How works Test new features Press Copyright Contact us Creatorsこの問題に答えるためには,辺の比が1: で,その間の角度が45°のときは,「1:1: の直角二等辺三角形になる」という中学校数学の基本が前もって分かっていなければなりません. このことに気
解析問題 二等辺三角形の内心からの2斜辺と底辺への垂線の延長線が 黄チャートex108が 』の部分まで分かるのですがそこからどのように変形すれば次の条件が成り立つとき,三角形は二等辺三角形になります。 三角形の2つの辺が等しい(定義) 三角形の2つの角が等しい 例題 無料動画講義(理論)
二等辺三角形になるための条件 証明のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
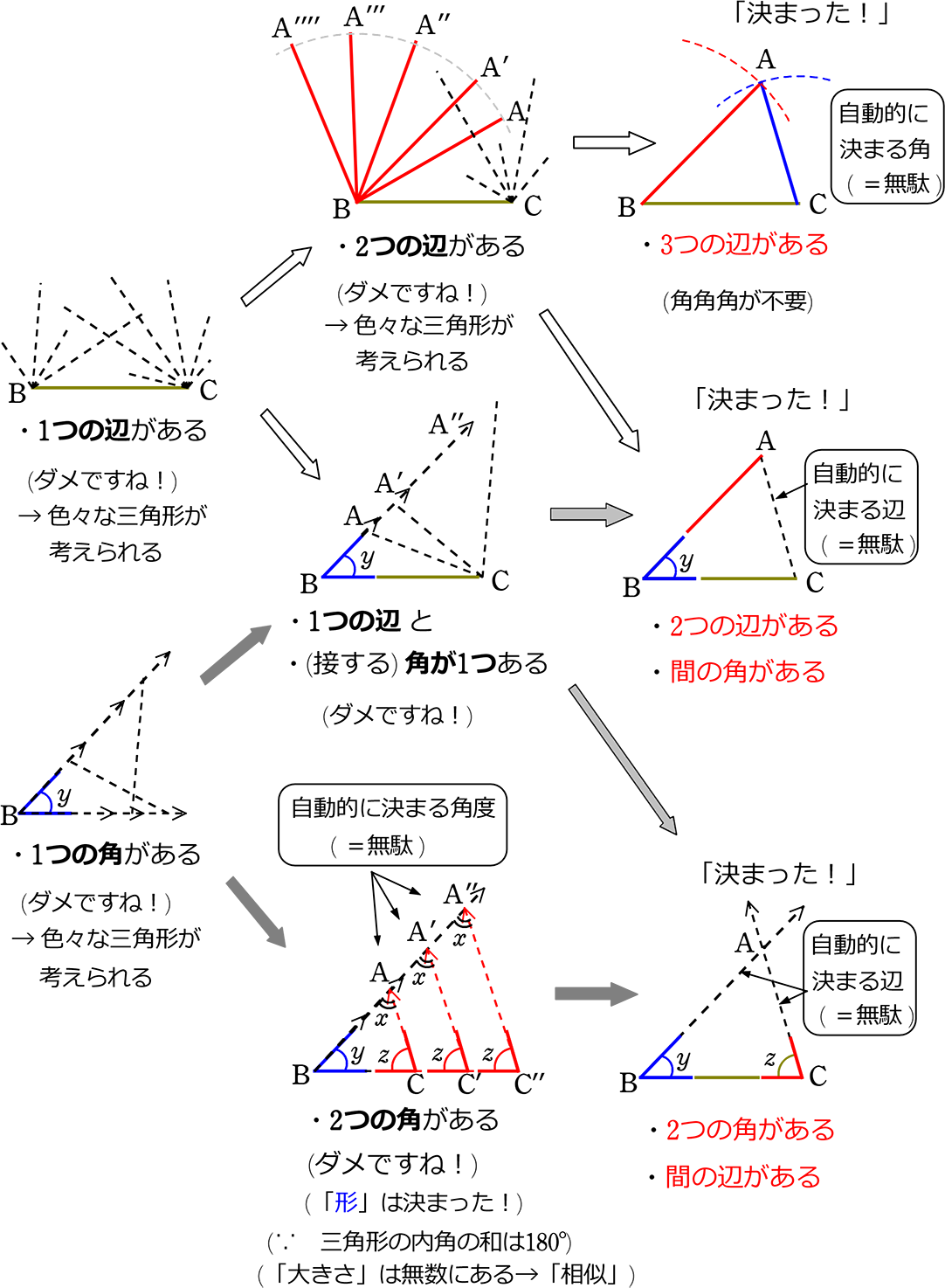 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
「二等辺三角形になるための条件 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 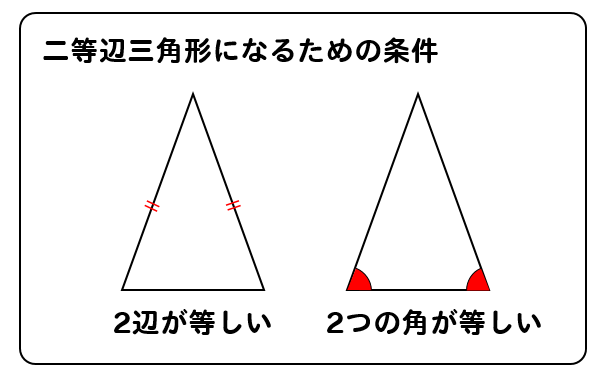 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
「二等辺三角形になるための条件 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 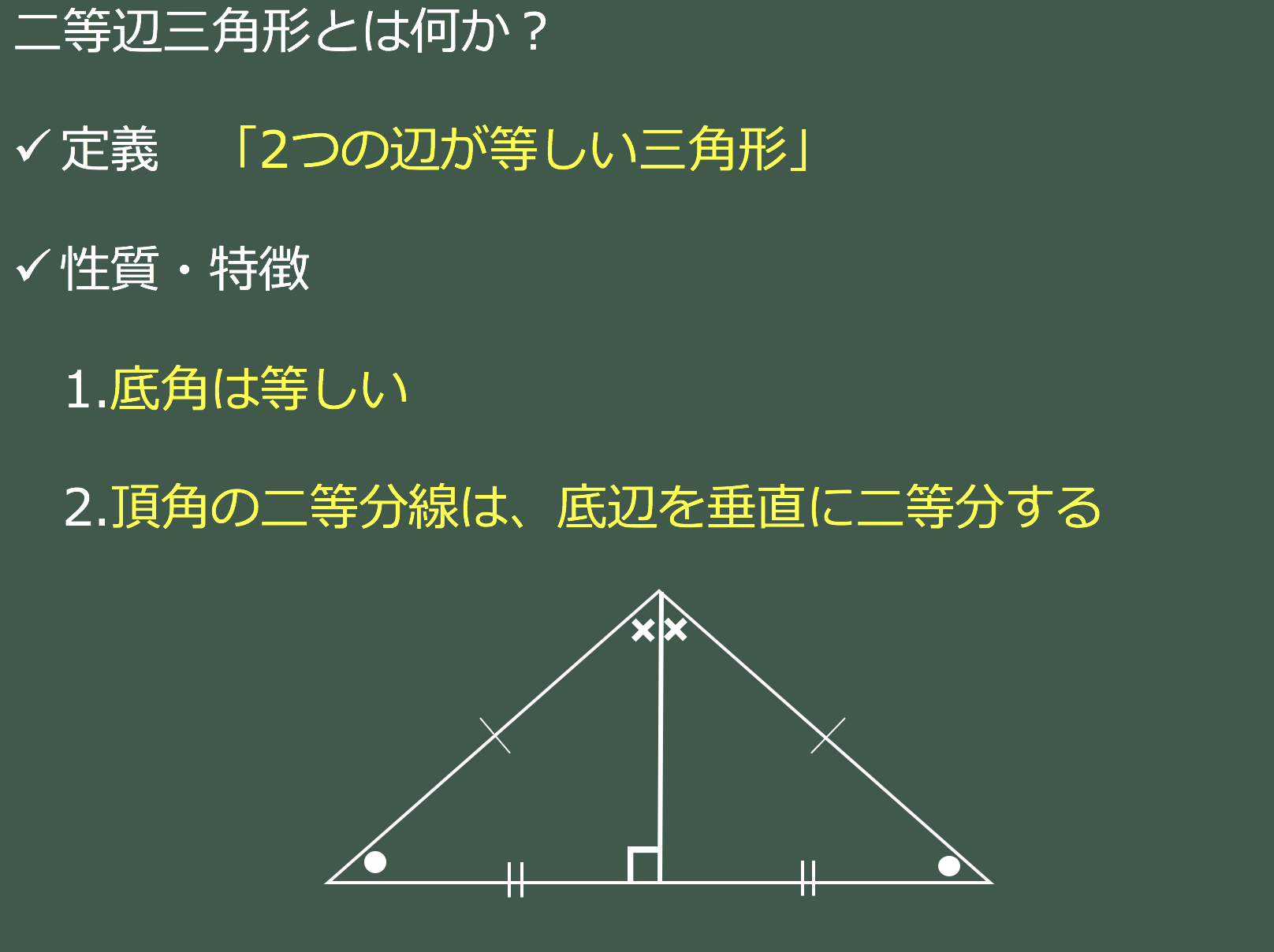 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 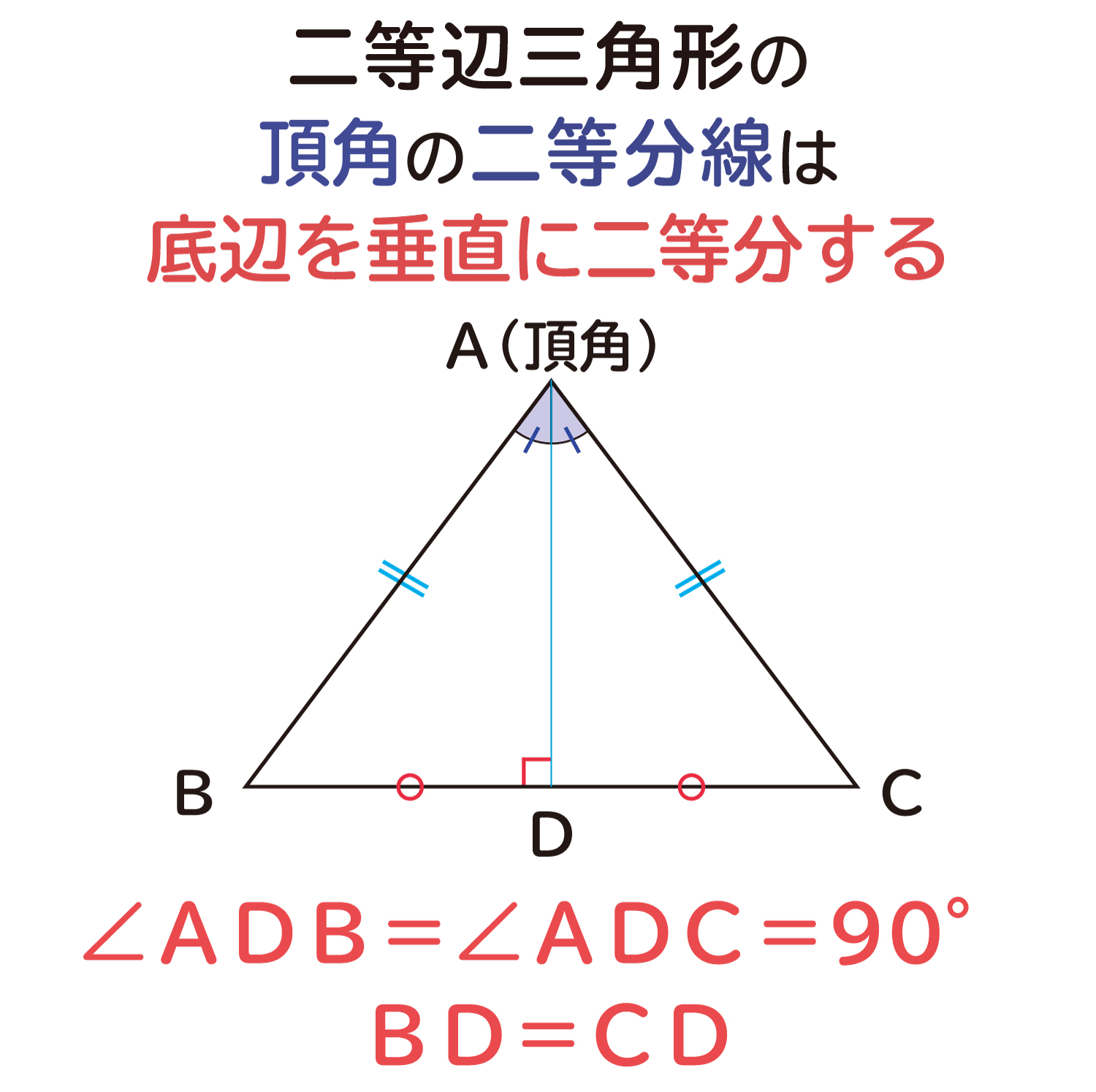 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
「二等辺三角形になるための条件 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
「二等辺三角形になるための条件 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 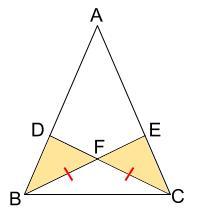 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
「二等辺三角形になるための条件 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
「二等辺三角形になるための条件 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 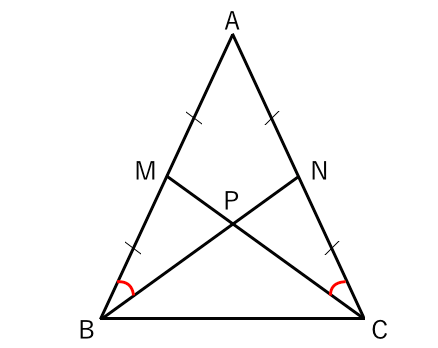 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 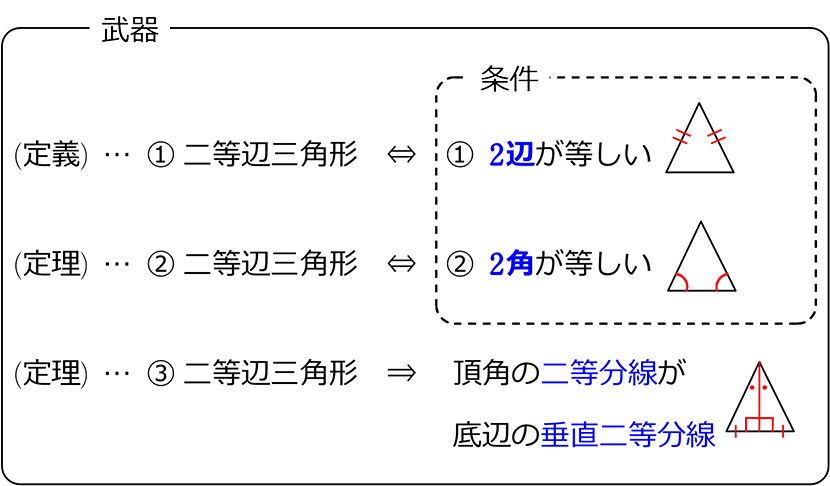 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 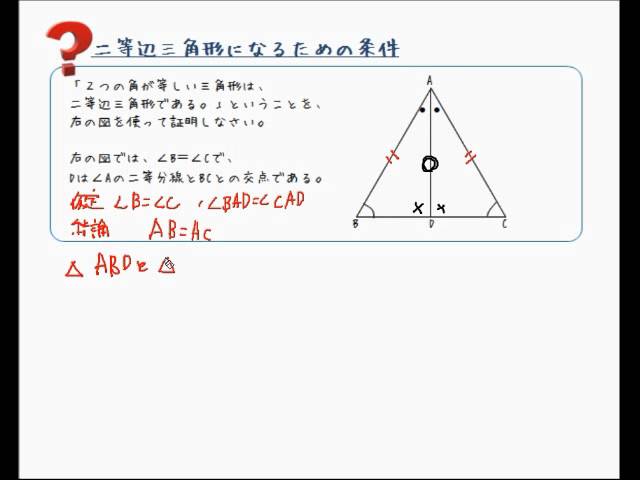 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
「二等辺三角形になるための条件 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 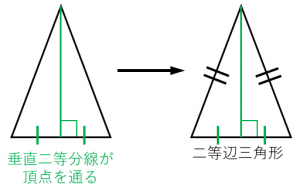 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 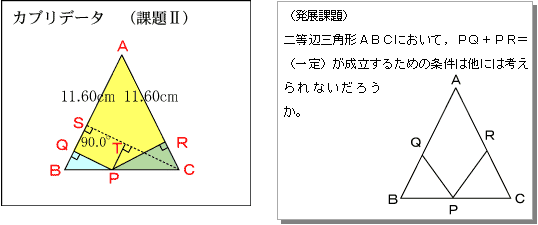 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
「二等辺三角形になるための条件 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 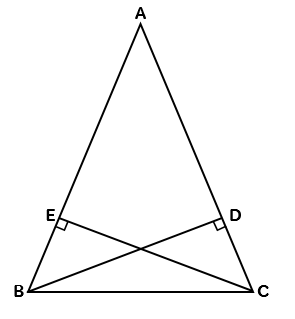 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
「二等辺三角形になるための条件 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
「二等辺三角形になるための条件 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 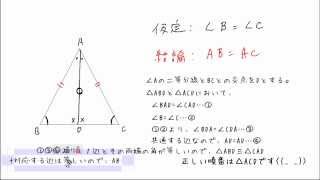 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
「二等辺三角形になるための条件 証明」の画像ギャラリー、詳細は各画像をクリックしてください。
中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 | 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |
 中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |  中学数学 なるための条件 って何 オンライン学習塾 啓理学舎 |





0 件のコメント:
コメントを投稿